Introduction

The experiments of parallel sorting algorithms are conducted on a e2-highcpu-32 (32 vCPUs, 32 GB) instance of the GCP.

Bubble Sort

The sequential and parallel bubble sort algorithm is implemented in a standard manner. While the array is not sorted iterate over it and swap the values next to each other according to the order. The parallel version contains two for-loops, one for swaps from even to odd index and one from odd to even. The complexity is of $O(n^2)$. The parallel version splits the for-loop into a number of chunk that is equal to $T$ the maximal number of available threads. After the parallel for-loop, a sequential for-loop performs possible swap operations between the last element and the first element of two adjacent chunks. This for-loop is smaller then the number of threads and is therefore not important for the complexity. To move the biggest element to the last position takes at most $T$ iterations. A few unnecessary operation could be conducted, for example given an revers-order, where in the last chunk a rather small would be moved to the end, but the number of such operations is bound and thus the complexity stay in $O(n^2)$ and we can expect speed-ups using parallelism.

Merge Sort

The sequential merge sort has a complexity of $O(n~log~n)$. The parallel version of the recursive algorithm executes the two recursive calls in parallel with $omp$ $tasks$. Before merging the two, the sub-arrays have to be sorted. The merging operation it self is not parallelized, which would be possible but only relevant to complete the first recursive calls and out of scope for this work. Thus the speed-up with $n$ threads will be below $n$. To not generated to small and to may tasks and therefore unnecessary overhead, we include a threshold on the problem size that stops not to split the the recursion for two parallel tasks.

Its best not to create more tasks when all threads are processing, thus the threshold for the size is $size/T$ for the recursive generation of tasks, as we can assume that tasks of the same recursion level have similar running times.

We modified the provided $merge$ function to use memory that is allocated in the beginning and given as second pointer argument, to not waist time on the initialization of memory inside the $merger$ function. This modification accelerated the merge sort overall.

Odd Even Sort

The odd-even sort algorithm is performing two for-loops, the first one only considering swap operations from even to odd indices and the second only from odd to even. Because the swap operations in the for-loops have no dependencies to each other they can be easily parallelized.

To parallelize the two for-loop we used for each a static scheduling that splits the for-loop in $m$ equally large chunks corresponding to the $m$ threads.

Quick sort

The parallel quick sort algorithm splits the array in to a number of chunk corresponding to the maximal number of threads and applies quick sort in parallel on these sub-arrays. Then they are merge together in pairs of two, as in the merge sort algorithm. This gave good results but we could do better and implemented a true parallel quicksort.

We implemented the quicksort algorithm from scratch, because using the $qsort$ function of $<stdlib.h>$ meant to slower the quick sort algorithm when paralleling with merge operations. We compared both variants and with our implementation of quicksort we achieve greater speedups and the sequential execution is fast by a factor of $1.4$ to $qsort$. As in the merge sort we us a threshold depending on the number of omp-threads to decide where or not to open new $tasks$:

    threshold = N/num_threads;

    void true_parallel_quick_sort(*T, lo, hi){
        if (hi - lo < threshold/4){
            true_quick_sort(T, lo, hi);
            return ; 
        }
        if (lo < hi){
            while (1)
            {
                while (T[i]<pivot){i++;}
                while (T[j]>pivot){j--;}
                if (i >= j){break;}
                tmp = T[i]; T[i] = T[j]; T[j] = tmp;
                i++; j--;
            }
            #pragma omp task
            true_parallel_quick_sort(T, lo, j);
            #pragma omp task
            true_parallel_quick_sort(T, j+1, hi); 
        }
    }

Performance

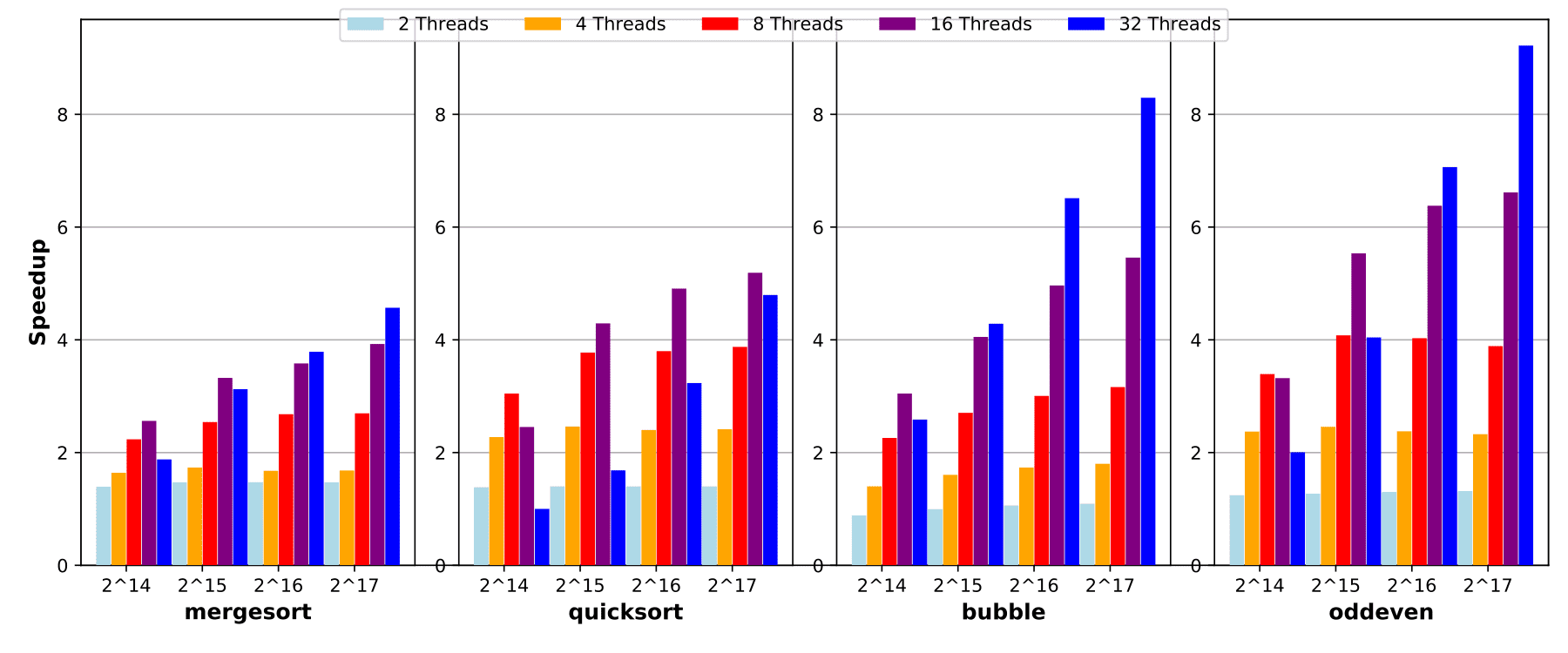
We compare the four different sorting algorithms in the following regarding their speedups and efficiency for increasing numbers of CPUs. The experiments are conducted with 2, 4, 8, 16, and 32 $openMP$ Threads and for uint64 arrays of size $2^2, 2^3, ..., 2^{29}$ for merge- and quicksort and with array sizes of $2^2, 2^3, ..., 2^{18}$ for bubble and odd-even sort.

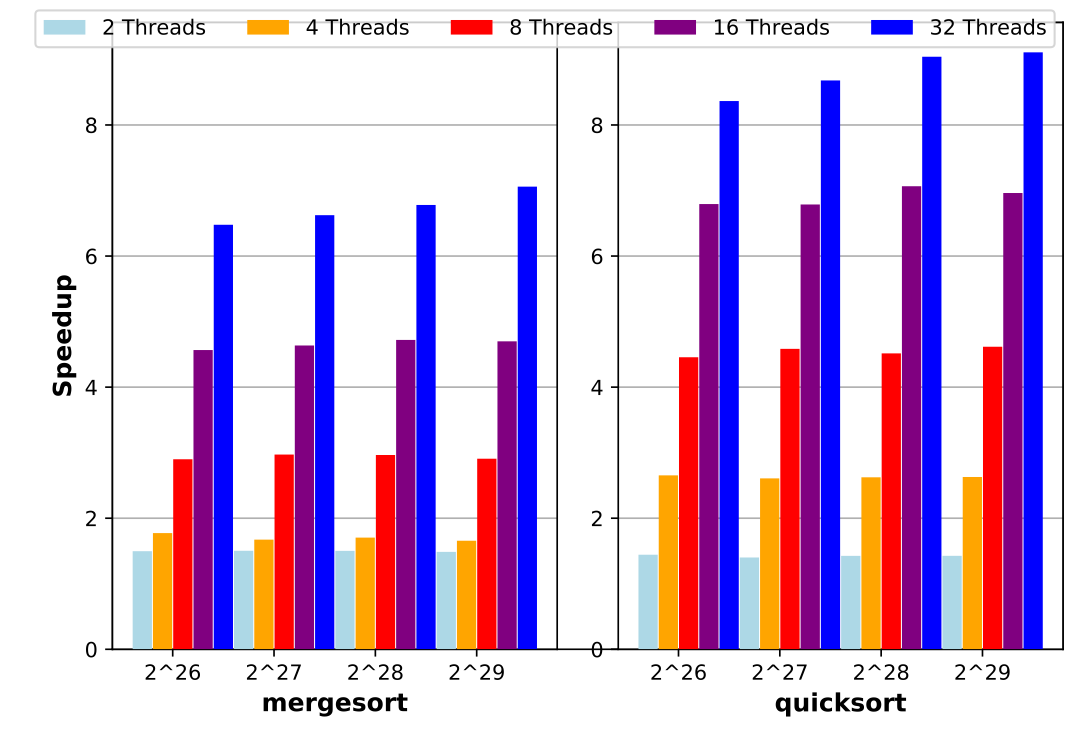
Figure 1 shows that the parallel merge and quicksort algorithm for the array sizes of $2^{14}, ..., 2^{17}$ yields rather small speedup, because the running time is still short and thus the omp-overhead proportionally large. The efficiency decreases rapidly with increasing number of threads. Figure 4 illustrates that parallelisation becomes beneficial only for very large arrays and consequently longer running times. For arrays of size $2 ^{13}$ multi-threading starts to pay-off for all sorting algorithms, see Figure 6.

Conclusion

Evaluating the algorithms for speedups and total running time, the parallel quicksort outperforms in both categories. In general the results show that recursive algorithms can have an advantage over iterative algorithms such as bubble and odd-even sort because their for loop iteration as a fast as their slowest chunk of the for-loop. Quicksort might pivot on an non-ideal element but this causes no other threads to wait. Hence when the first $n$ partition are performed then all $n$ threads will continuously work until the array is sorted. The merge sort has such an dependency which sparks in Figure 2. Besides mergesort needs twice as much memory. Concerning the $O(n^2)$ algorithms, even-though it is more straightforward to implement a parallel odd-even sort then a parallel bubble sort, the speedup advantage of odd-even is small.