Introduction

The work for this lab presents six different parallel implementations of the CFD (Computational Fluid Dynamic) simulation with Open MPI and compares them for weak and strong scaling. There are different methods to simulate a fluid. This project is using an implementation of the Lattice Boltzmann Method (LBM) which is easy to parallelize in distributed memory systems.

1D Splitting

For the 1D splitting, it is ensured that all sub-domains have the same size, therefore the execution aborts with exit(1) when the total width is not dividable by the number of processes. The ranks of the MPI processes correspond to the sub-domains of the mash from left to right in increasing order. The processes communicate the continuous columns on the borders of the domain to their predecessor and successor.

Exercise 1. Two cases are distinguished here, the processes of rank 0 have no communication to the left and process with the highest rank, that is comm_size , to the right. Otherwise, processes receive first from the left and then respond, then the communication to the right starts by sending first. As blocking communication is used, this results in a dependency for the processes from 0 to comm_size , which should yield lower speed-ups. Let us see how it behaves later in section 3.

Exercise 2. With an odd-even distinction, the dependency path from Exercise 1 is decreased to the interdependence between processes of odd and even ranks. First, the processes with an even rank send and then receives from odd ranks. The edge cases are handled as in Exercise 1.

Exercise 3. To further decrease dependency the communication to the left and right processes is performed here with non-blocking communication. Once all four column exchanges to place independently of each other, the simulation calculation continues, this is ensured with MPI_Waitall() after all non-blocking send and receives.

2D Splitting

The 2D splitting is performed with MPI_Dims_create that decides on the number of sub-domains along x and y, such that these are all of equal size. Given the dimensions, the communication card is created and each process receives its coordinates by the following MPI function, in the variable coords . Where we use the initialized communicator, periods are disabled and the reorder of ranks is allowed.

// with dimsG = {0,0}; we set no constraints on the dimension
MPI_Dims_create(comm_size, 2, dimsGiven);
MPI_Cart_create(MPI_COMM_WORLD, 2, dimsGiven, periodsGiven,
                            reorderGiven, &(comm->communicator));
MPI_Cart_get(comm->communicator, 2, dimsRecv, periodsRecv, coords);

For prim-numbers, this is always one-dimensional. In case that total width or height is not dividable by the assigned number of processes along the dimension, then all processes are reassigned along the x-dimension, and we fall back to 1D.

Now that vertical row exchange will be implemented, which is non-continues memory here, 4 buffers are allocated to send and receive rows of the mash between sub-domains.

Exercise 4. For this exercise, the edge cases are handle by MPI_PROC_NULL as target rank in the communication. A function is therefore implemented get_rank that resolves the 2D coordinates of the sub-domains to the assigned rank when the coordinates are outside the mesh, MPI_PROC_NULL is returned. Another function computes the four neighbors of the process. Diagonal communication is unnecessary because the correct reception of the corner cells is ensured by first performing the vertical and then the horizontal communication.

For readability, the communication is performed by a function that decides for all possibilities providing action (send, recv) and direction (top, bottom, left, right) type. For top and bottom communication, two functions handle the transfer from the mesh row to and from the buffer that is used to send and receive rows. For the communication odd and even coordinates are distinguished, for x and y even receives first and odd sends.

Exercise 5. MPI provides types for non-continuous memory, that are used here instead, and the perform_action function from exercise 4 is accordingly modified. The code becomes a little easier to read but we should not expect speedups, as MPI will not do any magic.

Exercise 6. Here the communication is performed non-blocking in two blocks first vertical, then horizontal, in between the communication is blocked with MPI_Waitall . This way the corner cells are correctly transferred.

Experiments: Scalability measurement

The Experiments are performed with GCE on a cluster of 8 Instances of type e2-highcpu-4 that have 4 vCPUs¹ available. The maximum number of parallel processes to run is 32.

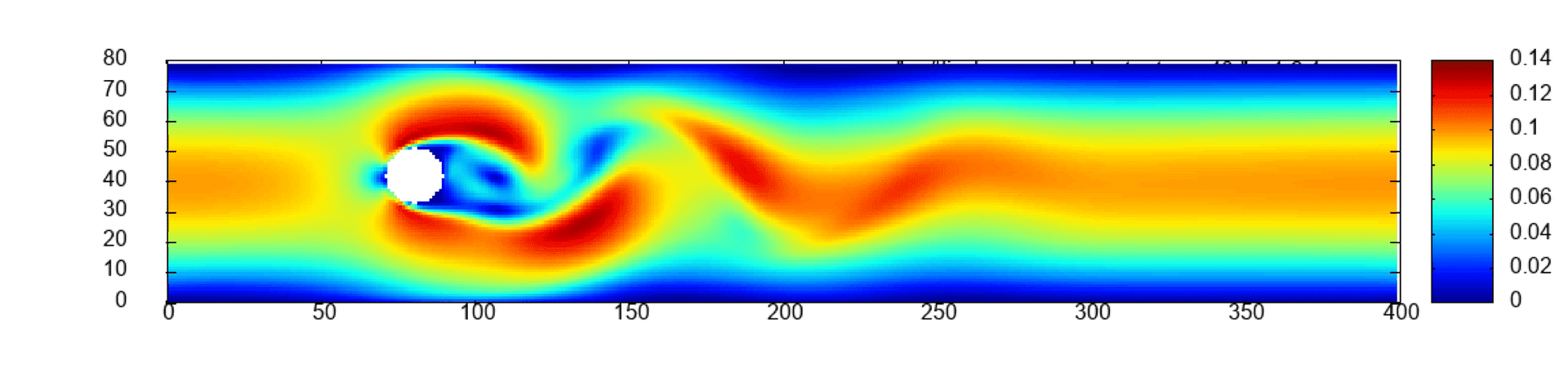
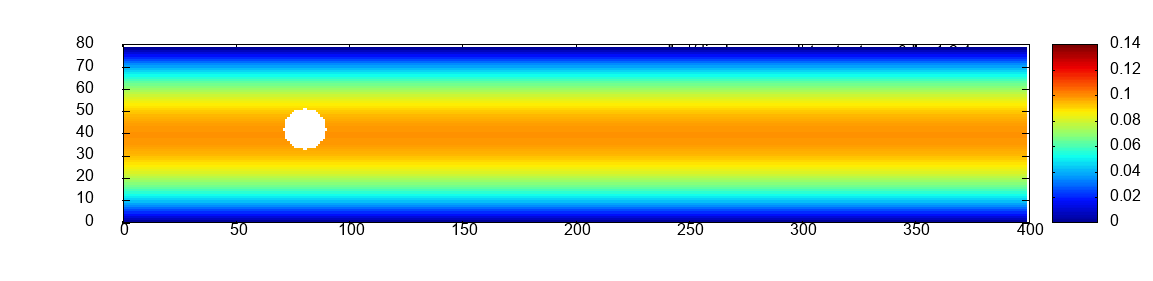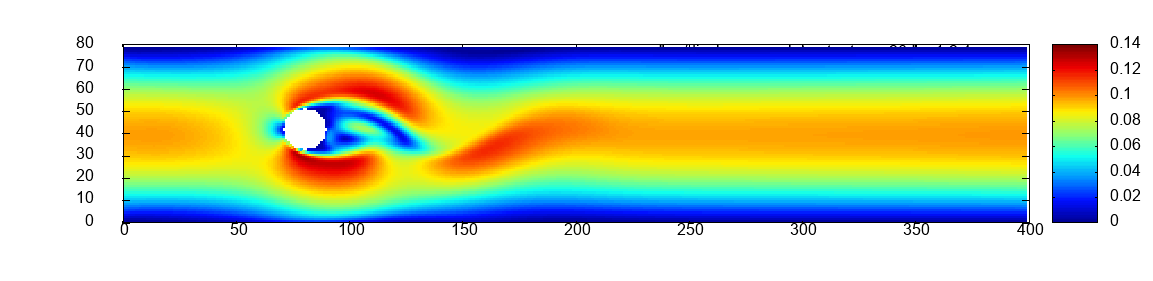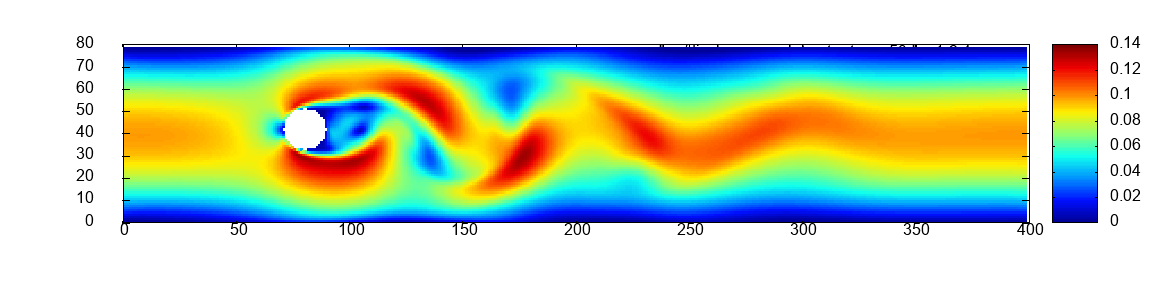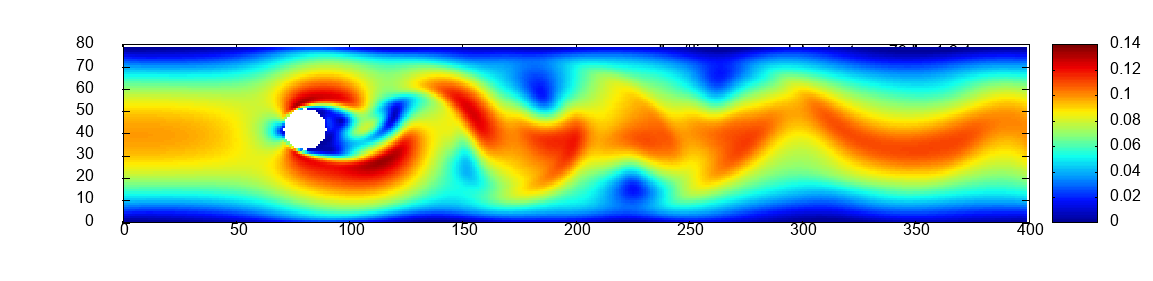
Two scalability experiments are carried out for all six exercises. First, strong scaling on a constant mesh of size $980 \times 194$ which is the initial mesh of $400 \times 80$ scaled by a factor of 6, see Figure 1 in the middle. Second, weak scaling. The mesh of $400 \times 80$ and the number of processes are scaled jointly by the same factor, illustrated in the middle of Figure 1.

The results for exercises 1 and 4 are not displayed as the legend in Figure 1 indicates because they performed equally to exercise 2 and 5, respectively. For the odd-even communication pattern in exercise 2, a speedup was expected compare to exercise 1 because the dependency chain is now reduced from comm_size to 2. This is true as much as the last process has to wait in the first iteration for all other processes to finish communication. But the process of lower rank starts computing after finishing its communication with the next process. Therefore processes only wait on the start-up. Then they are slightly shifted and synchronized so that only in the last iteration the first process stops working before, which is the only drawback. Thus in the meantime, the computation is fully parallelized, and there is no speedup difference to the odd-even pattern for multiple iterations.

The results for exercises 4 and 5 the forecast was accurate that the MPI_Type_vector is not better than the implemented method to copy from and to the buffer for vertical communication.

Apart from that, there is 1D and 2D Splitting to compare. Figure 1 on the left shows that the blocking and non-blocking implementation of 1D splitting is faster than this 2D splitting counterpart. That relates to the fact that the communication in 1D happens in continuous memory, which is faster because of the extra copy operation for non-continuous memory. In addition, is the number of communicated cells mostly greater in the 2D splitting. It was shown that the 1D splitting communicates (for 32 processes) a height of 450, and 2D splitting a height plus width of 400, where 286 cells are non-continuous memory. The 2D splitting could be further optimized, trying to keep the width shorter or equal to the height, minimizing continuous communication (width) and circumference of the sub-domain. Such an approach is not part of this work, as its advantages are limited.

The non-blocking communication in exercises 3 and 6 shows its advantage more explicitly. The 1D splitting remains faster, besides the time spent on copying cells for exercise 6, it has to communicate the two directions vertical and horizontal communication sequentially, to ensure correct calculations for the corners of the sub-domains.

Overall the parallelization of the CFD simulation is successful, and the speedups are close to the number of processes, see Figure 1 in the middle and on the right for the speedups for exercise 3. One observation that is pointing out here, is that from 16 to 14 processes, and indeed it is the same for 17 processes, the running time almost doubles, and the speedup for 32 processes is just above 14. This behavior indicates that there are some shared resources on the instances, that are only available twice. Hence the third process is then blocked, which blocks, in consequence, the other processes. Notably, each MPI process runs on a virtual CPU where one core is hyperthreaded, that compute in parallel but shares resources such a memory².

Conclusion

The different implementations have illustrated various strategies to parallelize simulations. Even though the 1D non-blocking implementation outperformed the other tactics for the presented experiments, for more extensive simulations with more than 64 cores, the 2D splitting can reduce the communication significantly, and advantages can be anticipated with vast confidence.